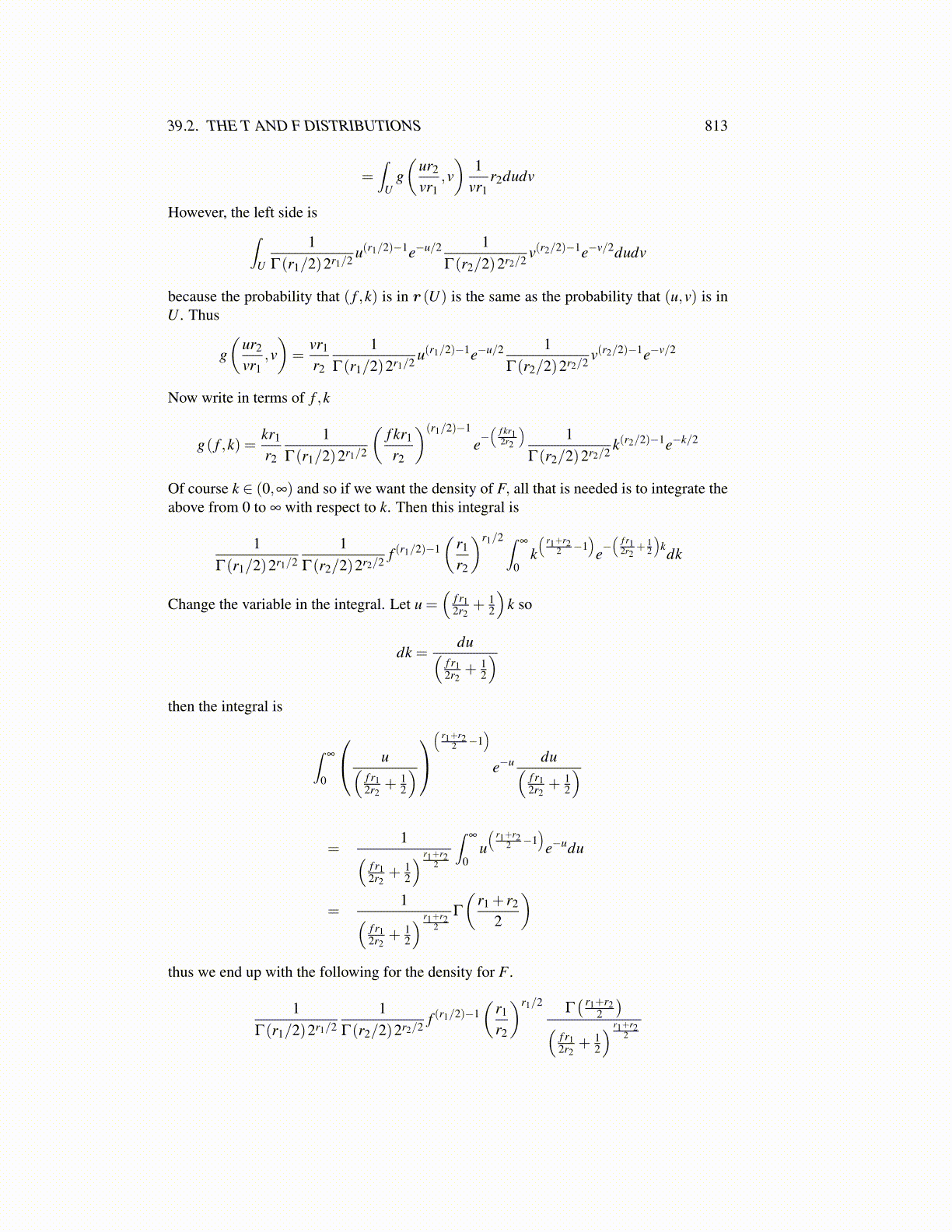
39.2. THE T AND F DISTRIBUTIONS 813
=∫
Ug(
ur2
vr1,v)
1vr1
r2dudv
However, the left side is∫U
1Γ(r1/2)2r1/2 u(r1/2)−1e−u/2 1
Γ(r2/2)2r2/2 v(r2/2)−1e−v/2dudv
because the probability that ( f ,k) is in r (U) is the same as the probability that (u,v) is inU . Thus
g(
ur2
vr1,v)=
vr1
r2
1Γ(r1/2)2r1/2 u(r1/2)−1e−u/2 1
Γ(r2/2)2r2/2 v(r2/2)−1e−v/2
Now write in terms of f ,k
g( f ,k) =kr1
r2
1Γ(r1/2)2r1/2
(f kr1
r2
)(r1/2)−1
e−(
f kr12r2
)1
Γ(r2/2)2r2/2 k(r2/2)−1e−k/2
Of course k ∈ (0,∞) and so if we want the density of F, all that is needed is to integrate theabove from 0 to ∞ with respect to k. Then this integral is
1Γ(r1/2)2r1/2
1Γ(r2/2)2r2/2 f (r1/2)−1
(r1
r2
)r1/2 ∫ ∞
0k(
r1+r22 −1
)e−(
f r12r2
+ 12
)kdk
Change the variable in the integral. Let u =(
f r12r2
+ 12
)k so
dk =du(
f r12r2
+ 12
)then the integral is
∫∞
0
u(f r12r2
+ 12
)(
r1+r22 −1
)e−u du(
f r12r2
+ 12
)
=1(
f r12r2
+ 12
) r1+r22
∫∞
0u(
r1+r22 −1
)e−udu
=1(
f r12r2
+ 12
) r1+r22
Γ
(r1 + r2
2
)
thus we end up with the following for the density for F .
1Γ(r1/2)2r1/2
1Γ(r2/2)2r2/2 f (r1/2)−1
(r1
r2
)r1/2Γ( r1+r2
2
)(
f r12r2
+ 12
) r1+r22