8.10. EXERCISES 189

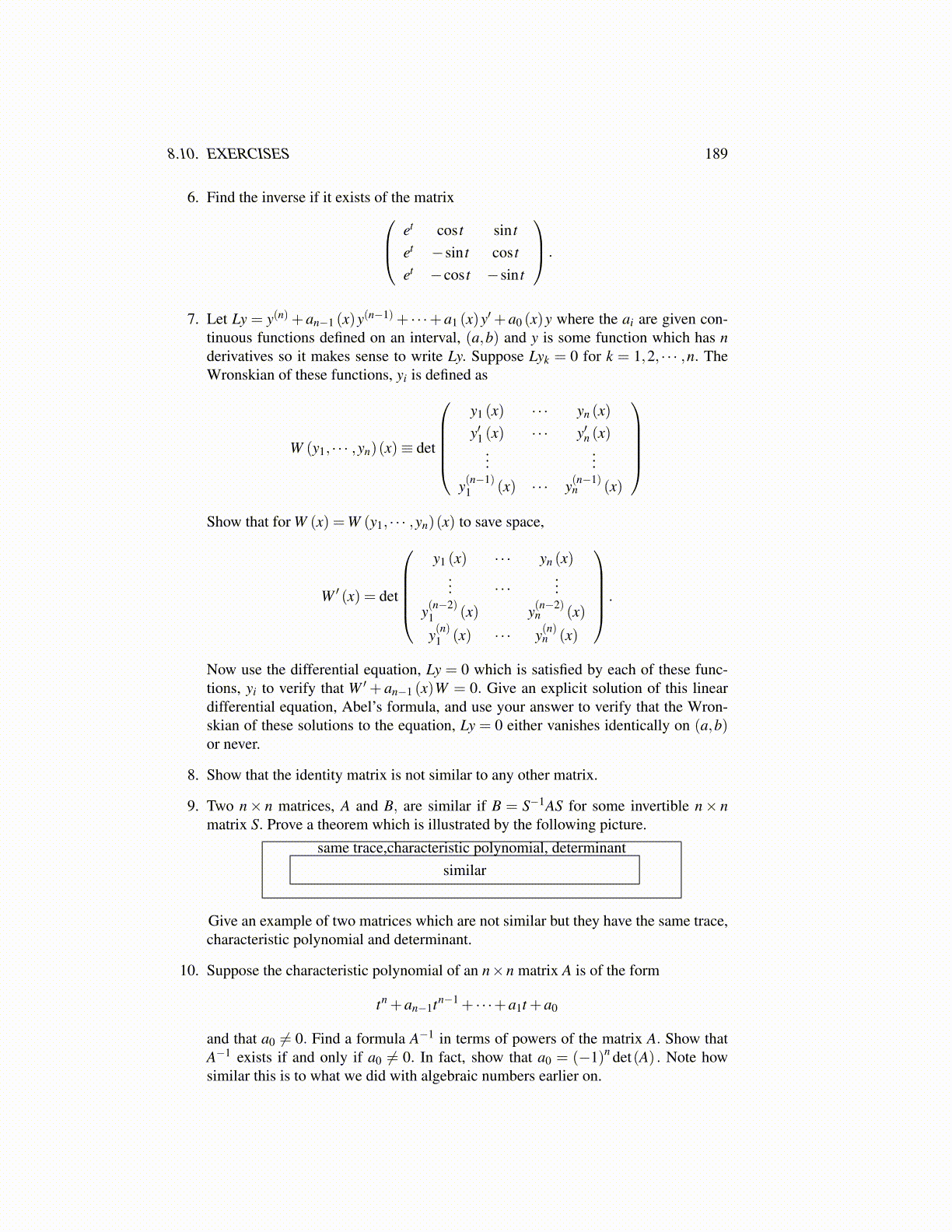
6. Find the inverse if it exists of the matrix et cos t sin tet −sin t cos tet −cos t −sin t

 .

7. Let Ly = y(n)+ an−1 (x)y(n−1)+ · · ·+ a1 (x)y′+ a0 (x)y where the ai are given con-tinuous functions defined on an interval, (a,b) and y is some function which has nderivatives so it makes sense to write Ly. Suppose Lyk = 0 for k = 1,2, · · · ,n. TheWronskian of these functions, yi is defined as

W (y1, · · · ,yn)(x)≡ det

y1 (x) · · · yn (x)y′1 (x) · · · y′n (x)

......

y(n−1)1 (x) · · · y(n−1)

n (x)

Show that for W (x) =W (y1, · · · ,yn)(x) to save space,

W ′ (x) = det

y1 (x) · · · yn (x)

... · · ·...

y(n−2)1 (x) y(n−2)

n (x)

y(n)1 (x) · · · y(n)n (x)

 .

Now use the differential equation, Ly = 0 which is satisfied by each of these func-tions, yi to verify that W ′+ an−1 (x)W = 0. Give an explicit solution of this lineardifferential equation, Abel’s formula, and use your answer to verify that the Wron-skian of these solutions to the equation, Ly = 0 either vanishes identically on (a,b)or never.

8. Show that the identity matrix is not similar to any other matrix.

9. Two n× n matrices, A and B, are similar if B = S−1AS for some invertible n× nmatrix S. Prove a theorem which is illustrated by the following picture.

similarsame trace,characteristic polynomial, determinant

Give an example of two matrices which are not similar but they have the same trace,characteristic polynomial and determinant.

10. Suppose the characteristic polynomial of an n×n matrix A is of the form

tn +an−1tn−1 + · · ·+a1t +a0

and that a0 ̸= 0. Find a formula A−1 in terms of powers of the matrix A. Show thatA−1 exists if and only if a0 ̸= 0. In fact, show that a0 = (−1)n det(A) . Note howsimilar this is to what we did with algebraic numbers earlier on.