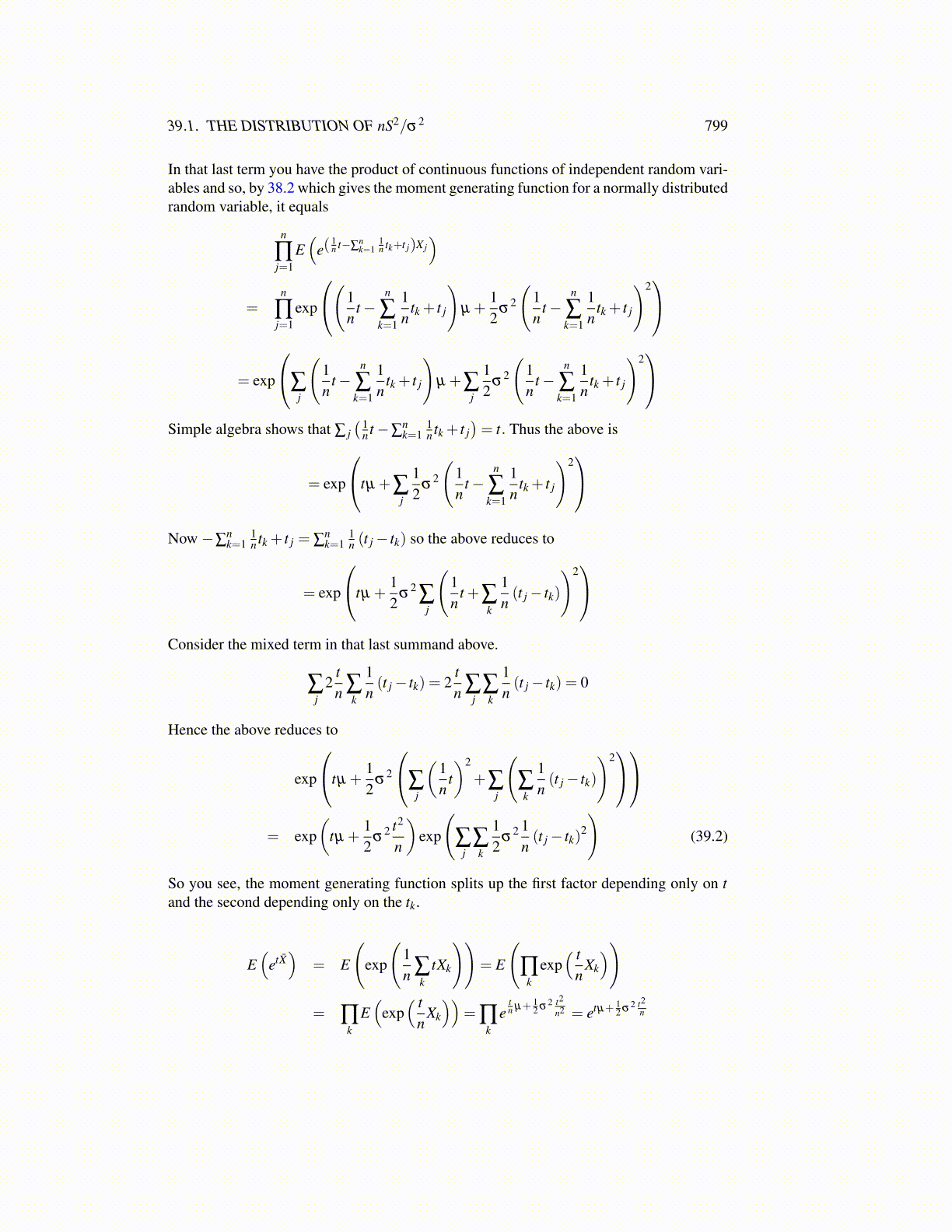
39.1. THE DISTRIBUTION OF nS2/σ2 799

In that last term you have the product of continuous functions of independent random vari-ables and so, by 38.2 which gives the moment generating function for a normally distributedrandom variable, it equals

n

∏j=1

E(

e(1n t−∑

nk=1

1n tk+t j)X j

)

=n

∏j=1

exp

(1n

t−n

∑k=1

1n

tk + t j

)µ +

12

σ2

(1n

t−n

∑k=1

1n

tk + t j

)2

= exp

∑j

(1n

t−n

∑k=1

1n

tk + t j

)µ +∑

j

12

σ2

(1n

t−n

∑k=1

1n

tk + t j

)2

Simple algebra shows that ∑ j( 1

n t−∑nk=1

1n tk + t j

)= t. Thus the above is

= exp

tµ +∑j

12

σ2

(1n

t−n

∑k=1

1n

tk + t j

)2

Now −∑nk=1

1n tk + t j = ∑

nk=1

1n (t j− tk) so the above reduces to

= exp

tµ +12

σ2∑

j

(1n

t +∑k

1n(t j− tk)

)2

Consider the mixed term in that last summand above.

∑j

2tn ∑

k

1n(t j− tk) = 2

tn ∑

j∑k

1n(t j− tk) = 0

Hence the above reduces to

exp

tµ +12

σ2

∑j

(1n

t)2

+∑j

(∑k

1n(t j− tk)

)2

= exp(

tµ +12

σ2 t2

n

)exp

(∑

j∑k

12

σ2 1

n(t j− tk)

2

)(39.2)

So you see, the moment generating function splits up the first factor depending only on tand the second depending only on the tk.

E(

etX̄)

= E

(exp

(1n ∑

ktXk

))= E

(∏

kexp( t

nXk

))

= ∏k

E(

exp( t

nXk

))= ∏

ke

tn µ+ 1

2 σ2 t2

n2 = etµ+ 12 σ2 t2

n