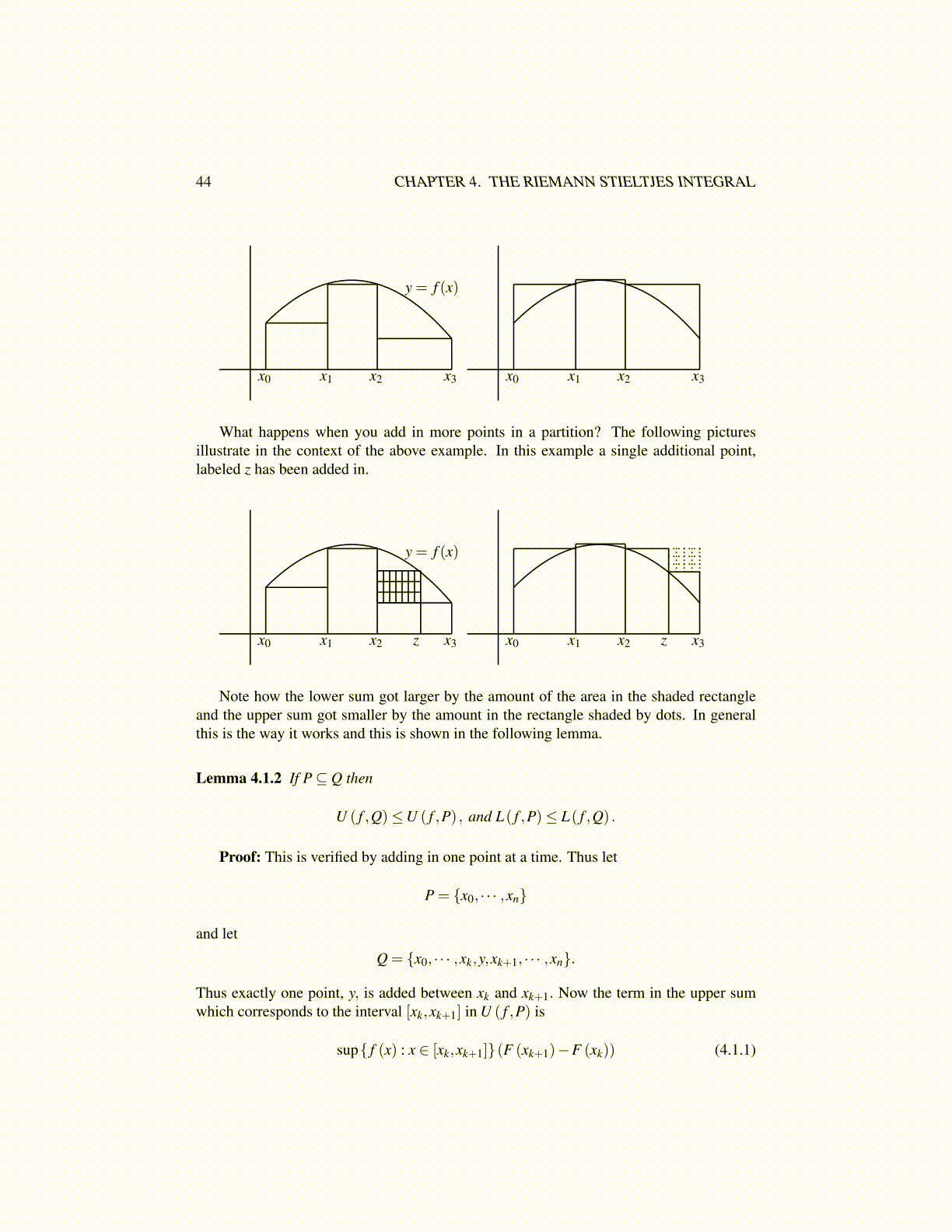
44 CHAPTER 4. THE RIEMANN STIELTJES INTEGRAL

y = f (x)

x0 x1 x2 x3 x0 x1 x2 x3

What happens when you add in more points in a partition? The following picturesillustrate in the context of the above example. In this example a single additional point,labeled z has been added in.

y = f (x)

x0 x1 x2 x3z x0 x1 x2 x3z

Note how the lower sum got larger by the amount of the area in the shaded rectangleand the upper sum got smaller by the amount in the rectangle shaded by dots. In generalthis is the way it works and this is shown in the following lemma.

Lemma 4.1.2 If P⊆ Q then

U ( f ,Q)≤U ( f ,P) , and L( f ,P)≤ L( f ,Q) .

Proof: This is verified by adding in one point at a time. Thus let

P = {x0, · · · ,xn}

and let

Q = {x0, · · · ,xk,y,xk+1, · · · ,xn}.

Thus exactly one point, y, is added between xk and xk+1. Now the term in the upper sumwhich corresponds to the interval [xk,xk+1] in U ( f ,P) is

sup{ f (x) : x ∈ [xk,xk+1]}(F (xk+1)−F (xk)) (4.1.1)