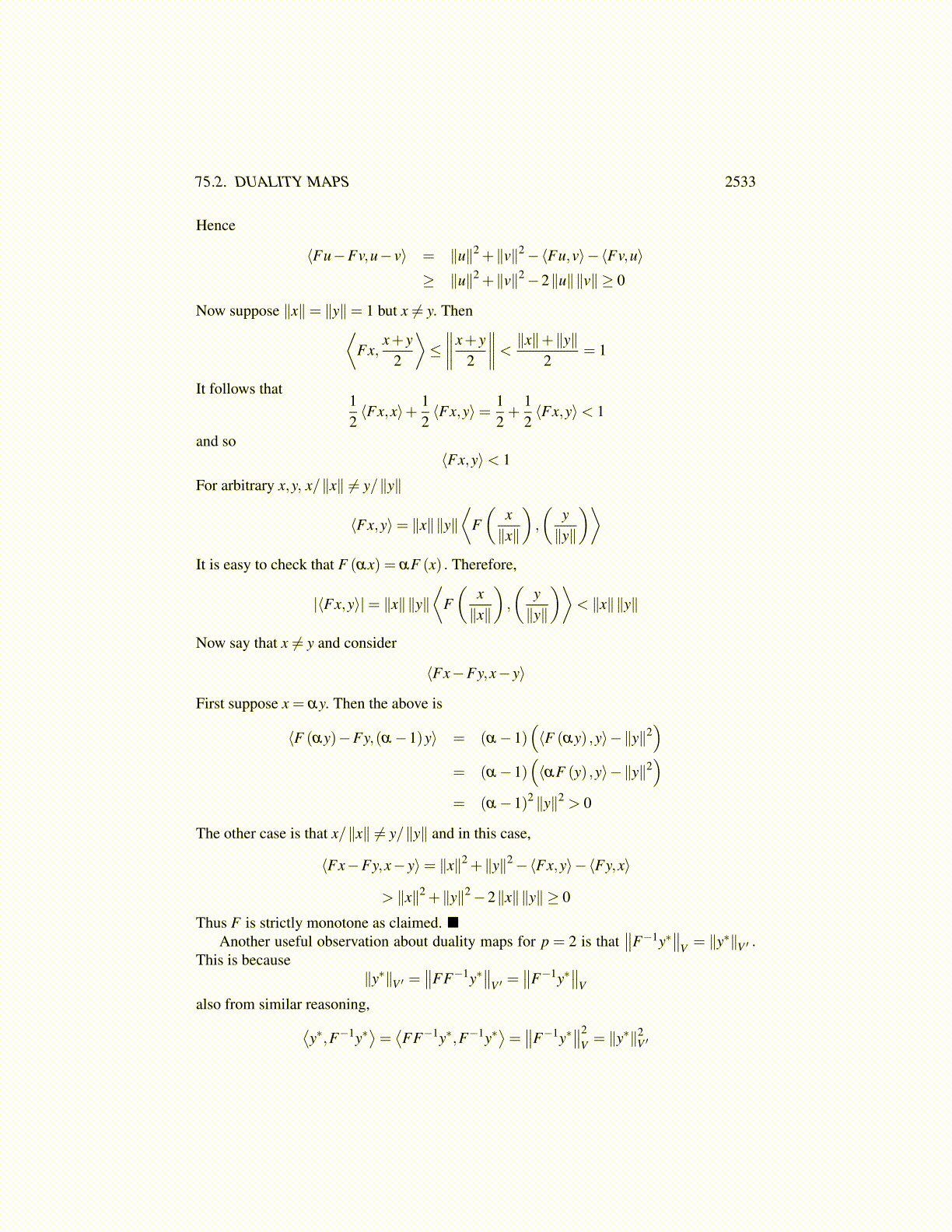
75.2. DUALITY MAPS 2533

Proof: Say xn→ x. Then does it follow that Fxn ⇀ Fx? Suppose not. Then there is asubsequence, still denoted as xn such that xn→ x but Fxn ⇀ y ̸= Fx where here ⇀ denotesweak convergence. This follows from the Eberlein Smulian theorem. Then

⟨y,x⟩= limn→∞⟨Fxn,xn⟩= lim

n→∞∥xn∥2 = ∥x∥2

Also, there exists z,∥z∥= 1 and ⟨y,z⟩ ≥ ∥y∥− ε. Then

∥y∥− ε ≤ ⟨y,z⟩= limn→∞⟨Fxn,z⟩ ≤ lim inf

n→∞∥Fxn∥= lim inf

n→∞∥xn∥= ∥x∥

and since ε is arbitrary, ∥y∥ ≤ ∥x∥ . It follows from the above construction of Fx, thaty = Fx after all, a contradiction.

Theorem 75.2.3 Let X be a reflexive Banach space with X ′ having strictly convex norm1.Then for p > 1, there exists a mapping F : X → X ′ which is bounded, monotone, hemi-continuous, coercive in the sense that lim|x|→∞ ⟨Fx,x⟩/ |x| = ∞, which also satisfies theinequalities

|⟨Fx,y⟩| ≤ |⟨Fx,x⟩|1/p′ |⟨Fy,y⟩|1/p

Note that these conclusions about duality maps show that they map onto the dual space.The duality map was onto and it was monotone. This was shown above. Consider the

form of a duality map for the Lp spaces. Let F : Lp→ (Lp)′ be the one which satisfies

||F f ||= || f ||p−1 , ⟨F f , f ⟩= || f ||p

Then in this case,F f = | f |p−2 f

This is because it does what it needs to do.

||F f ||Lp′ =

(∫Ω

(| f |p−1

)p′

dµ

)1/p′

=

(∫Ω

(| f |p/p′

)p′

dµ

)1/p′

=

(∫Ω

| f |p dµ

)1−(1/p)

=

((∫Ω

| f |p dµ

)1/p)p−1

= || f ||p−1Lp

while it is obvious that⟨F f , f ⟩=

∫Ω

| f |p dµ = || f ||pLp(Ω).

Now here is an interesting inequality which I will only consider in the case where thequantities are real valued.

Lemma 75.2.4 Let p > 2. Then for a,b real numbers,(|a|p−2 a−|b|p−2 b

)(a−b)≥C |a−b|p

for some constant C independent of a,b.1It is known that if the space is reflexive, then there is an equivalent norm which is strictly convex. However,

in most examples, this strict convexity is obvious.