144 CHAPTER 6. DIRECT SUMS AND BLOCK DIAGONAL MATRICES
If Vi = ker(L−µ iI)ki , then by definition, (Li−µ iI)
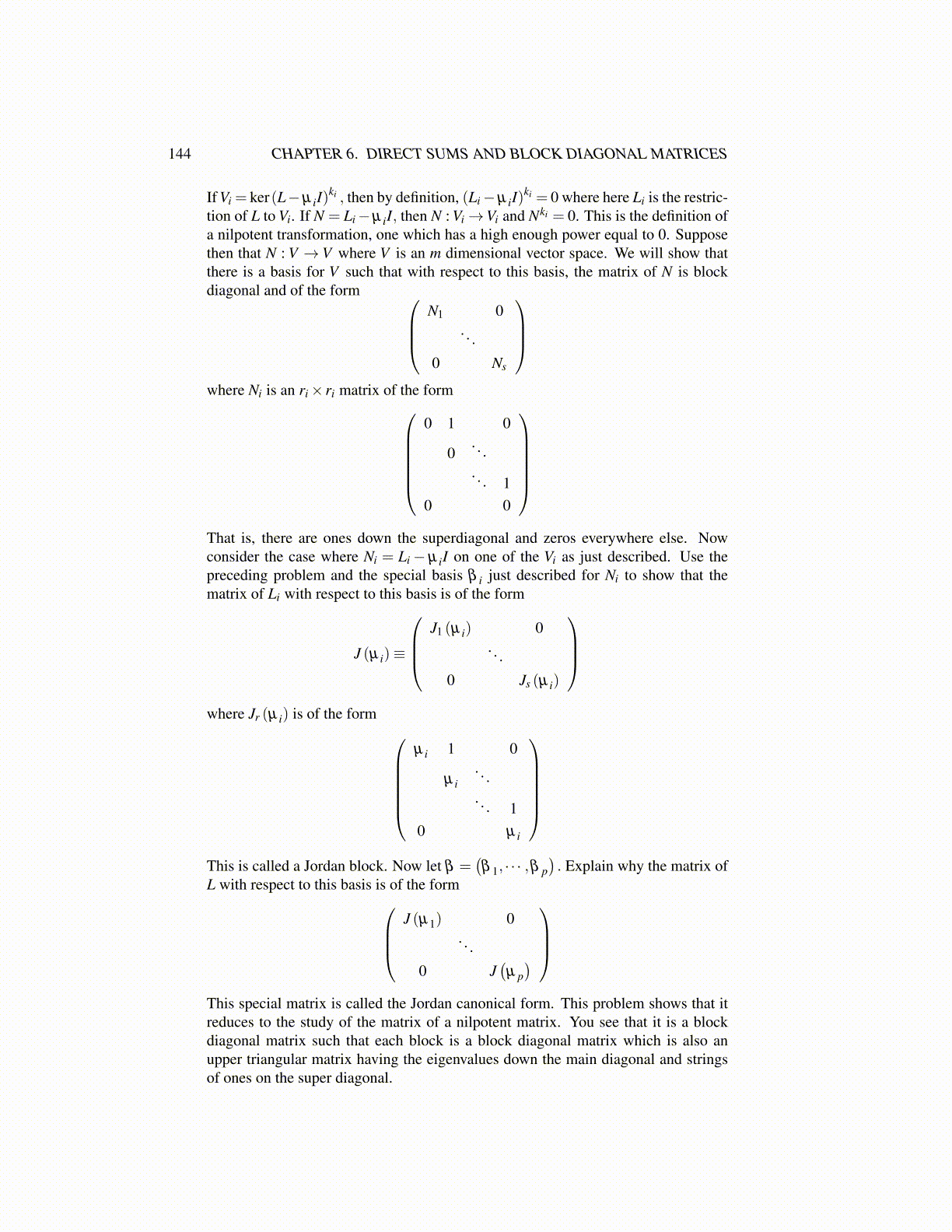
ki = 0 where here Li is the restric-tion of L to Vi. If N = Li−µ iI, then N : Vi→Vi and Nki = 0. This is the definition ofa nilpotent transformation, one which has a high enough power equal to 0. Supposethen that N : V → V where V is an m dimensional vector space. We will show thatthere is a basis for V such that with respect to this basis, the matrix of N is blockdiagonal and of the form
N1 0. . .
0 Ns
where Ni is an ri× ri matrix of the form
0 1 0
0. . .. . . 1
0 0
That is, there are ones down the superdiagonal and zeros everywhere else. Nowconsider the case where Ni = Li− µ iI on one of the Vi as just described. Use thepreceding problem and the special basis β i just described for Ni to show that thematrix of Li with respect to this basis is of the form
J (µ i)≡
J1 (µ i) 0
. . .
0 Js (µ i)
where Jr (µ i) is of the form
µ i 1 0
µ i. . .. . . 1
0 µ i
This is called a Jordan block. Now let β =
(β 1, · · · ,β p
). Explain why the matrix of
L with respect to this basis is of the formJ (µ1) 0
. . .
0 J(µ p)
This special matrix is called the Jordan canonical form. This problem shows that itreduces to the study of the matrix of a nilpotent matrix. You see that it is a blockdiagonal matrix such that each block is a block diagonal matrix which is also anupper triangular matrix having the eigenvalues down the main diagonal and stringsof ones on the super diagonal.