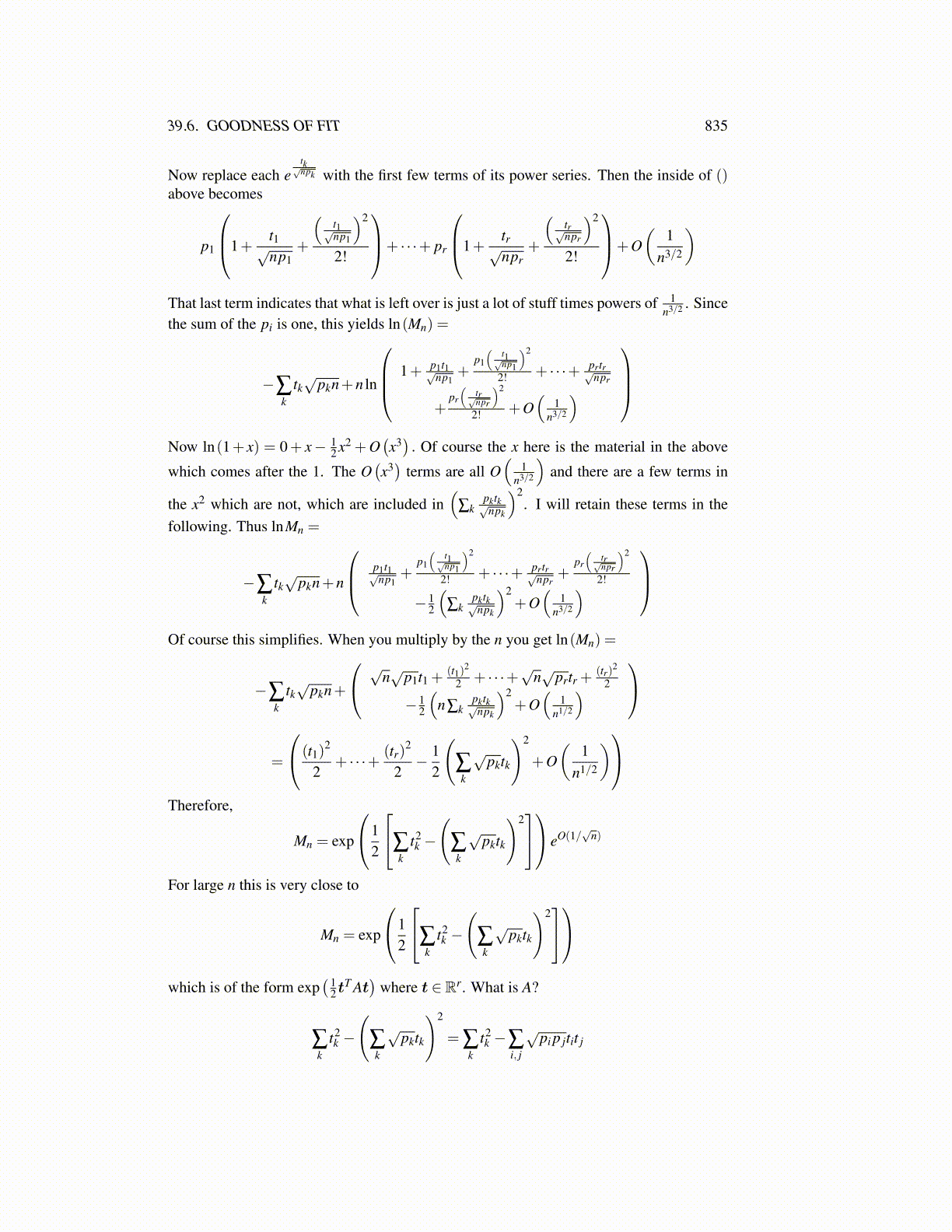
39.6. GOODNESS OF FIT 835
Now replace each etk√npk with the first few terms of its power series. Then the inside of ()
above becomes
p1
1+t1√np1
+
(t1√np1
)2
2!
+ · · ·+ pr
1+tr√npr
+
(tr√npr
)2
2!
+O(
1n3/2
)
That last term indicates that what is left over is just a lot of stuff times powers of 1n3/2 . Since
the sum of the pi is one, this yields ln(Mn) =
−∑k
tk√
pkn+n ln
1+ p1t1√np1
+p1
(t1√np1
)2
2! + · · ·+ prtr√npr
+pr
(tr√npr
)2
2! +O(
1n3/2
)
Now ln(1+ x) = 0+ x− 12 x2 +O
(x3). Of course the x here is the material in the above
which comes after the 1. The O(x3)
terms are all O(
1n3/2
)and there are a few terms in
the x2 which are not, which are included in(
∑kpktk√npk
)2. I will retain these terms in the
following. Thus lnMn =
−∑k
tk√
pkn+n
p1t1√np1
+p1
(t1√np1
)2
2! + · · ·+ prtr√npr
+pr
(tr√npr
)2
2!
− 12
(∑k
pktk√npk
)2+O
(1
n3/2
)
Of course this simplifies. When you multiply by the n you get ln(Mn) =
−∑k
tk√
pkn+
√n√
p1t1 +(t1)
2
2 + · · ·+√
n√
prtr +(tr)2
2
− 12
(n∑k
pktk√npk
)2+O
(1
n1/2
)
=
(t1)2
2+ · · ·+ (tr)
2
2− 1
2
(∑k
√pktk
)2
+O(
1n1/2
)Therefore,
Mn = exp
12
∑k
t2k −
(∑k
√pktk
)2eO(1/
√n)
For large n this is very close to
Mn = exp
12
∑k
t2k −
(∑k
√pktk
)2
which is of the form exp( 1
2tT At)
where t ∈ Rr. What is A?
∑k
t2k −
(∑k
√pktk
)2
= ∑k
t2k −∑
i, j
√pi p jtit j