38.8. MOMENT GENERATING FUNCTIONS 787
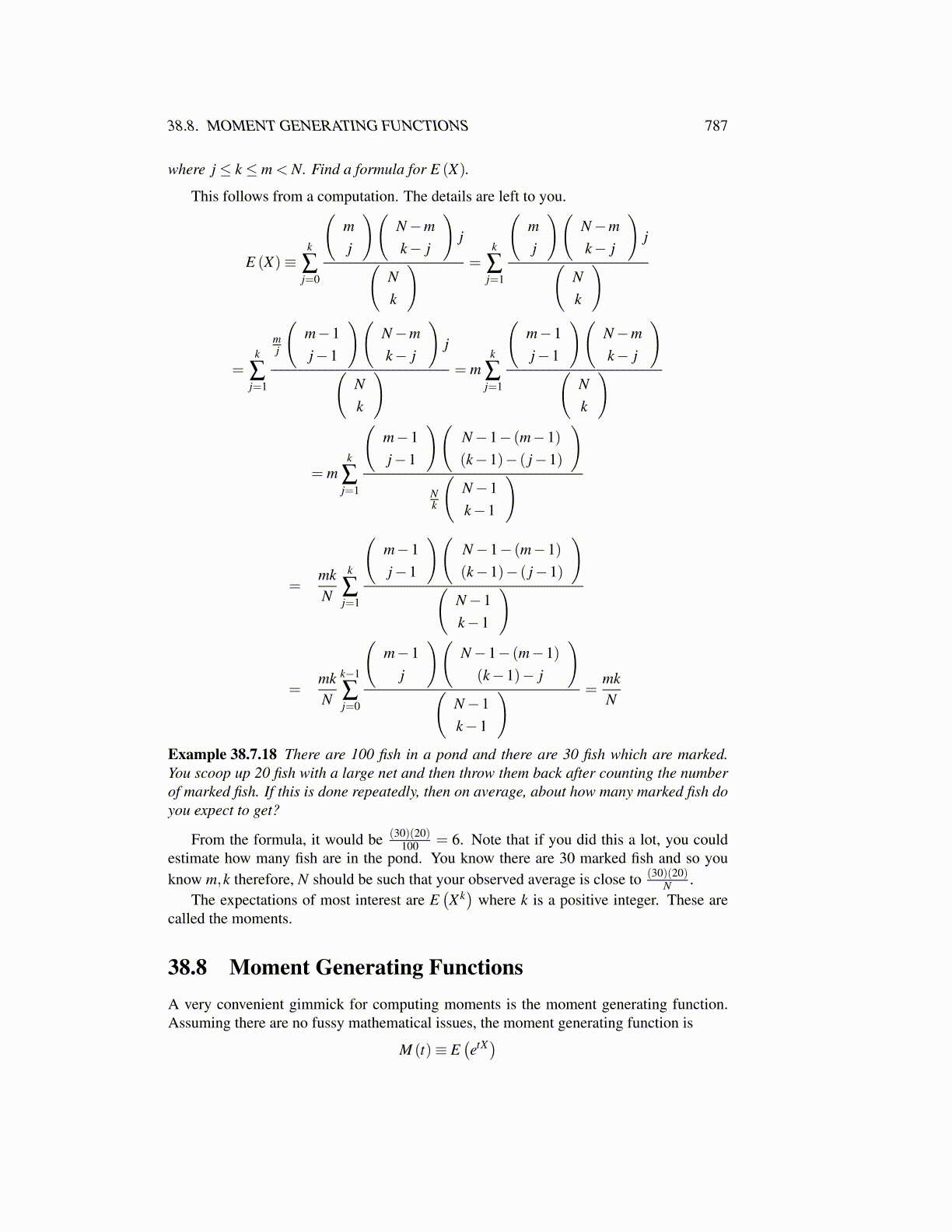
where j ≤ k ≤ m < N. Find a formula for E (X).
This follows from a computation. The details are left to you.
E (X)≡k
∑j=0
(mj
)(N−mk− j
)j(
Nk
) =k
∑j=1
(mj
)(N−mk− j
)j(
Nk
)
=k
∑j=1
mj
(m−1j−1
)(N−mk− j
)j(
Nk
) = mk
∑j=1
(m−1j−1
)(N−mk− j
)(
Nk
)
= mk
∑j=1
(m−1j−1
)(N−1− (m−1)(k−1)− ( j−1)
)Nk
(N−1k−1
)
=mkN
k
∑j=1
(m−1j−1
)(N−1− (m−1)(k−1)− ( j−1)
)(
N−1k−1
)
=mkN
k−1
∑j=0
(m−1
j
)(N−1− (m−1)
(k−1)− j
)(
N−1k−1
) =mkN
Example 38.7.18 There are 100 fish in a pond and there are 30 fish which are marked.You scoop up 20 fish with a large net and then throw them back after counting the numberof marked fish. If this is done repeatedly, then on average, about how many marked fish doyou expect to get?
From the formula, it would be (30)(20)100 = 6. Note that if you did this a lot, you could
estimate how many fish are in the pond. You know there are 30 marked fish and so youknow m,k therefore, N should be such that your observed average is close to (30)(20)
N .The expectations of most interest are E
(Xk)
where k is a positive integer. These arecalled the moments.
38.8 Moment Generating FunctionsA very convenient gimmick for computing moments is the moment generating function.Assuming there are no fussy mathematical issues, the moment generating function is
M (t)≡ E(etX)