5.4. LINES 57

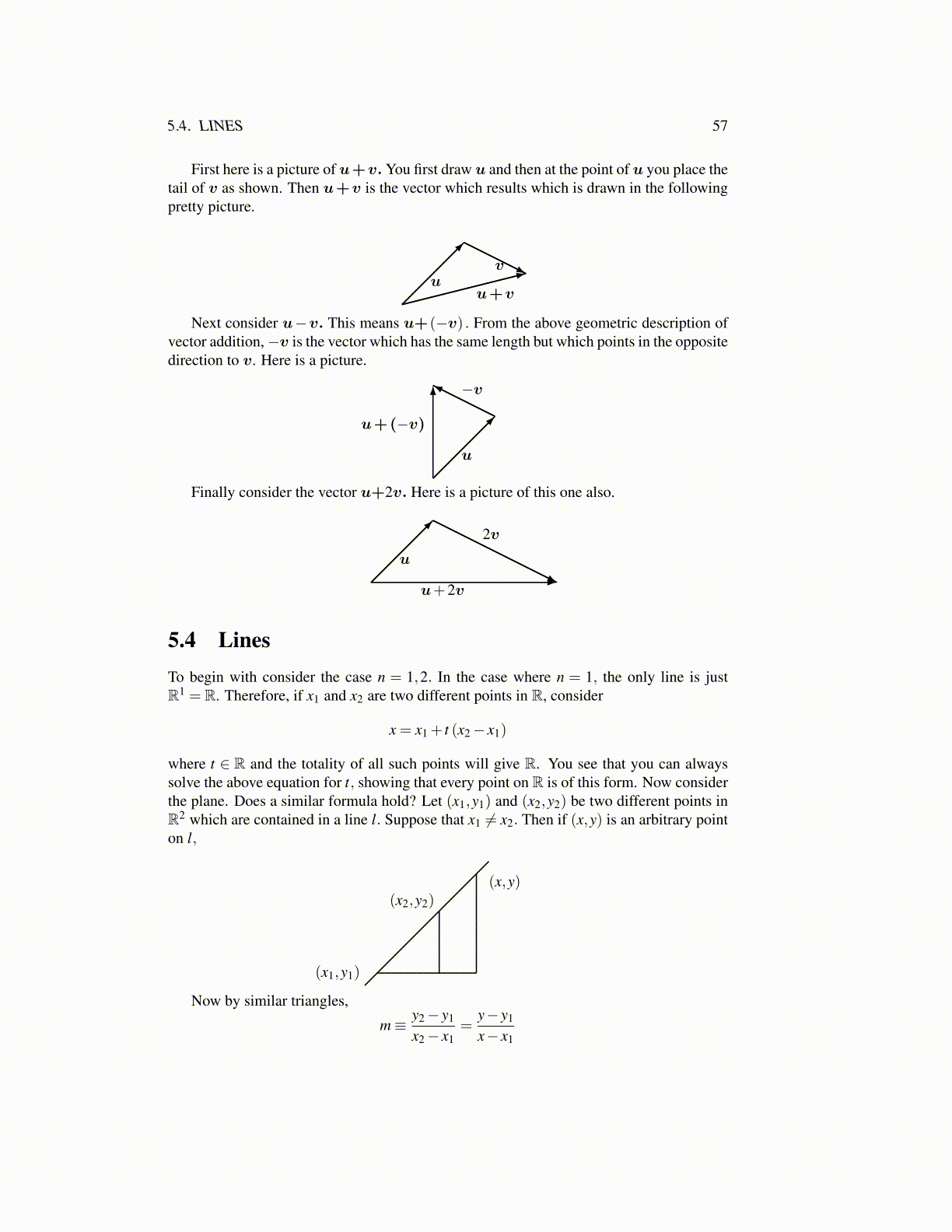
First here is a picture of u+v. You first draw u and then at the point of u you place thetail of v as shown. Then u+v is the vector which results which is drawn in the followingpretty picture.

uv

u+v

Next consider u−v. This means u+(−v) . From the above geometric description ofvector addition,−v is the vector which has the same length but which points in the oppositedirection to v. Here is a picture.

u

−v

u+(−v)

Finally consider the vector u+2v. Here is a picture of this one also.

u

2v

u+2v

5.4 LinesTo begin with consider the case n = 1,2. In the case where n = 1, the only line is justR1 = R. Therefore, if x1 and x2 are two different points in R, consider

x = x1 + t (x2− x1)

where t ∈ R and the totality of all such points will give R. You see that you can alwayssolve the above equation for t, showing that every point on R is of this form. Now considerthe plane. Does a similar formula hold? Let (x1,y1) and (x2,y2) be two different points inR2 which are contained in a line l. Suppose that x1 ̸= x2. Then if (x,y) is an arbitrary pointon l,

(x1,y1)

(x2,y2)(x,y)

Now by similar triangles,

m≡ y2− y1

x2− x1=

y− y1

x− x1