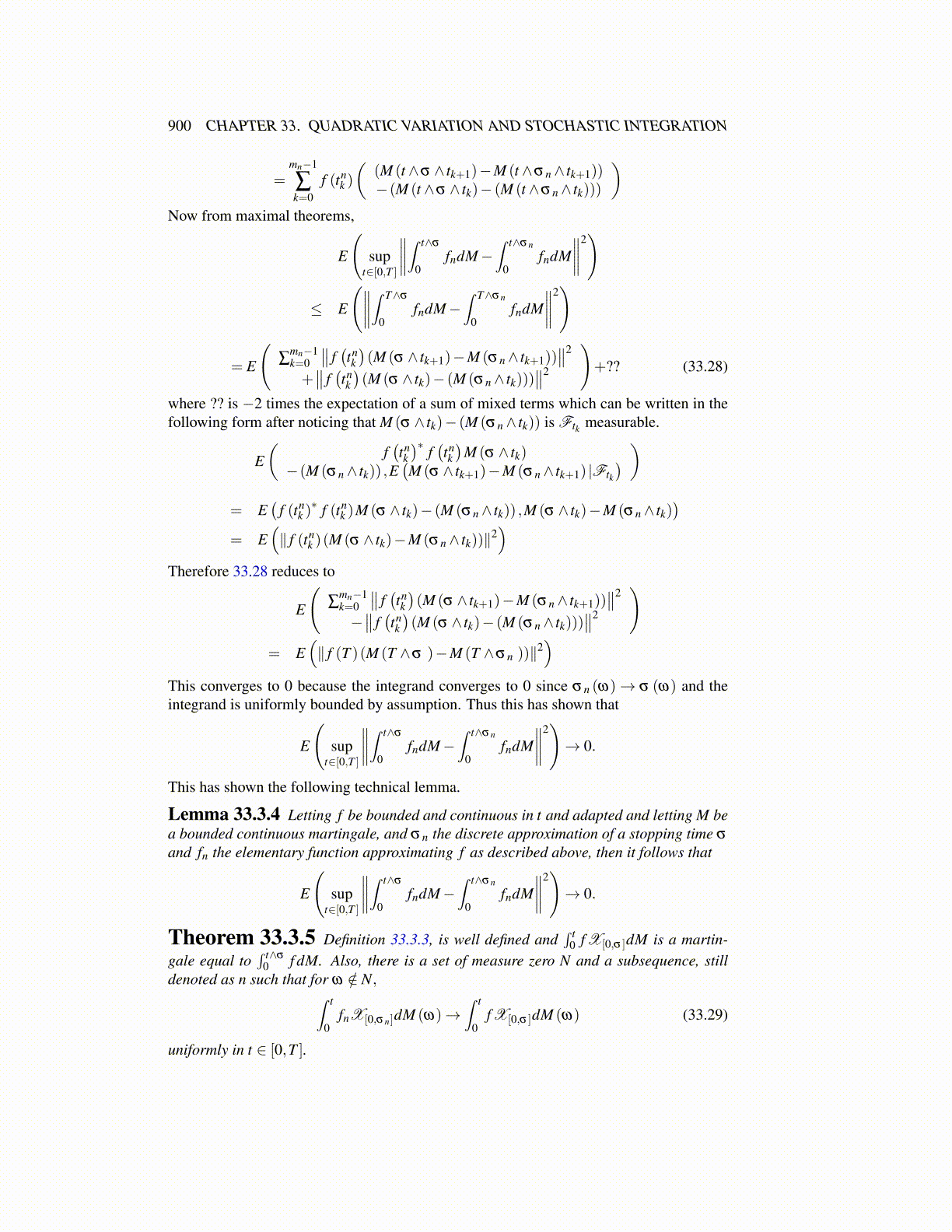
900 CHAPTER 33. QUADRATIC VARIATION AND STOCHASTIC INTEGRATION
=mn−1
∑k=0
f (tnk )
((M (t ∧σ ∧ tk+1)−M (t ∧σn∧ tk+1))−(M (t ∧σ ∧ tk)− (M (t ∧σn∧ tk)))
)Now from maximal theorems,
E
(sup
t∈[0,T ]
∥∥∥∥∫ t∧σ
0fndM−
∫ t∧σn
0fndM
∥∥∥∥2)
≤ E
(∥∥∥∥∫ T∧σ
0fndM−
∫ T∧σn
0fndM
∥∥∥∥2)
= E
(∑
mn−1k=0
∥∥ f(tnk
)(M (σ ∧ tk+1)−M (σn∧ tk+1))
∥∥2
+∥∥ f(tnk
)(M (σ ∧ tk)− (M (σn∧ tk)))
∥∥2
)+?? (33.28)
where ?? is −2 times the expectation of a sum of mixed terms which can be written in thefollowing form after noticing that M (σ ∧ tk)− (M (σn∧ tk)) is Ftk measurable.
E(
f(tnk
)∗ f(tnk
)M (σ ∧ tk)
−(M (σn∧ tk)) ,E(M (σ ∧ tk+1)−M (σn∧ tk+1) |Ftk
) )= E
(f (tn
k )∗ f (tn
k )M (σ ∧ tk)− (M (σn∧ tk)) ,M (σ ∧ tk)−M (σn∧ tk))
= E(∥ f (tn
k )(M (σ ∧ tk)−M (σn∧ tk))∥2)
Therefore 33.28 reduces to
E
(∑
mn−1k=0
∥∥ f(tnk
)(M (σ ∧ tk+1)−M (σn∧ tk+1))
∥∥2
−∥∥ f(tnk
)(M (σ ∧ tk)− (M (σn∧ tk)))
∥∥2
)= E
(∥ f (T )(M (T ∧σ )−M (T ∧σn ))∥2
)This converges to 0 because the integrand converges to 0 since σn (ω)→ σ (ω) and theintegrand is uniformly bounded by assumption. Thus this has shown that
E
(sup
t∈[0,T ]
∥∥∥∥∫ t∧σ
0fndM−
∫ t∧σn
0fndM
∥∥∥∥2)→ 0.
This has shown the following technical lemma.
Lemma 33.3.4 Letting f be bounded and continuous in t and adapted and letting M bea bounded continuous martingale, and σn the discrete approximation of a stopping time σ
and fn the elementary function approximating f as described above, then it follows that
E
(sup
t∈[0,T ]
∥∥∥∥∫ t∧σ
0fndM−
∫ t∧σn
0fndM
∥∥∥∥2)→ 0.
Theorem 33.3.5 Definition 33.3.3, is well defined and∫ t
0 f X[0,σ ]dM is a martin-gale equal to
∫ t∧σ
0 f dM. Also, there is a set of measure zero N and a subsequence, stilldenoted as n such that for ω /∈ N,∫ t
0fnX[0,σn]dM (ω)→
∫ t
0f X[0,σ ]dM (ω) (33.29)
uniformly in t ∈ [0,T ].