1.6. ELEMENTARY MATRICES 27
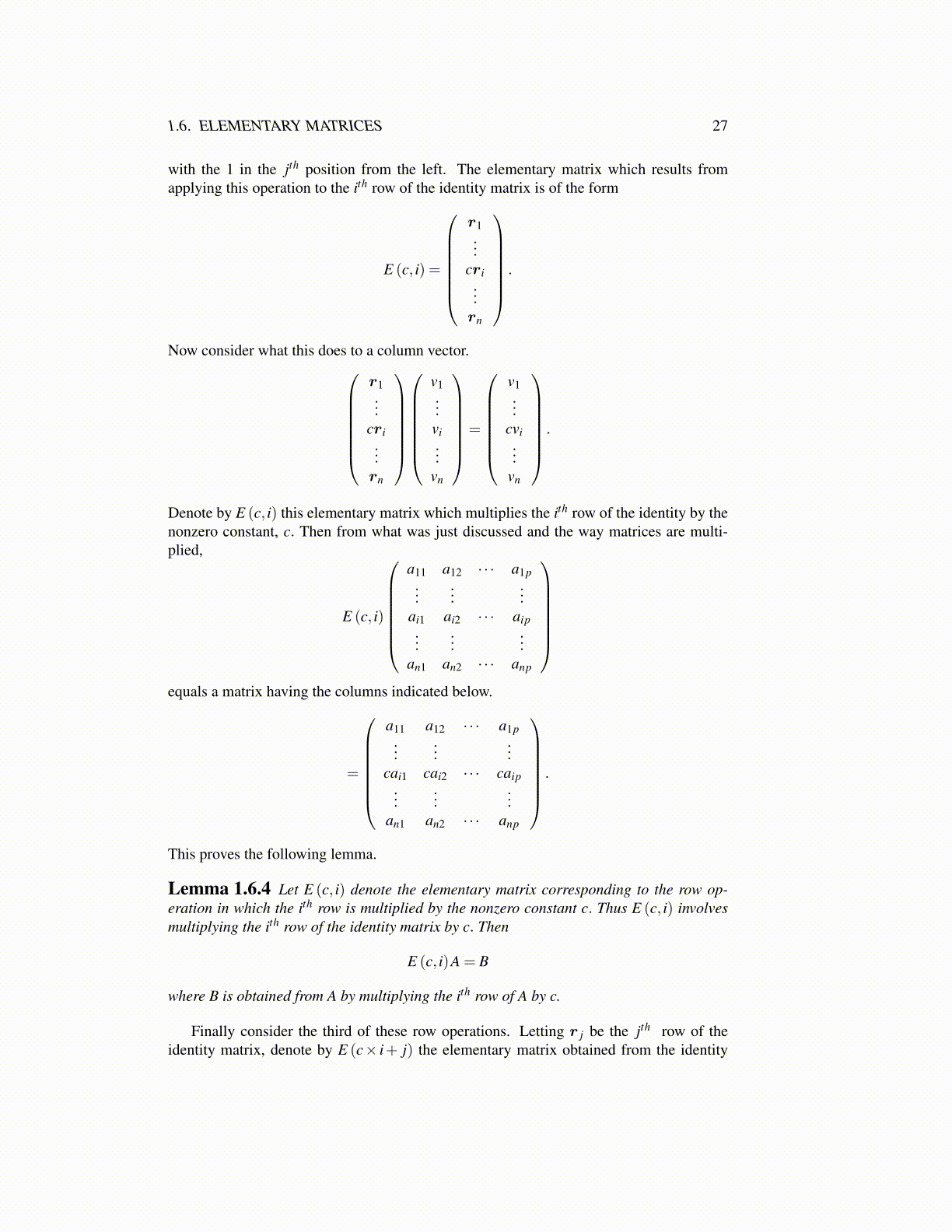
with the 1 in the jth position from the left. The elementary matrix which results fromapplying this operation to the ith row of the identity matrix is of the form
E (c, i) =
r1...
cri...rn
.
Now consider what this does to a column vector.r1...
cri...rn
v1...vi...
vn
=
v1...
cvi...
vn
.
Denote by E (c, i) this elementary matrix which multiplies the ith row of the identity by thenonzero constant, c. Then from what was just discussed and the way matrices are multi-plied,
E (c, i)
a11 a12 · · · a1p
......
...ai1 ai2 · · · aip...
......
an1 an2 · · · anp
equals a matrix having the columns indicated below.
=
a11 a12 · · · a1p
......
...cai1 cai2 · · · caip
......
...an1 an2 · · · anp
.
This proves the following lemma.
Lemma 1.6.4 Let E (c, i) denote the elementary matrix corresponding to the row op-eration in which the ith row is multiplied by the nonzero constant c. Thus E (c, i) involvesmultiplying the ith row of the identity matrix by c. Then
E (c, i)A = B
where B is obtained from A by multiplying the ith row of A by c.
Finally consider the third of these row operations. Letting r j be the jth row of theidentity matrix, denote by E (c× i+ j) the elementary matrix obtained from the identity