292 CHAPTER 12. THEOREMS INVOLVING LINE INTEGRALS
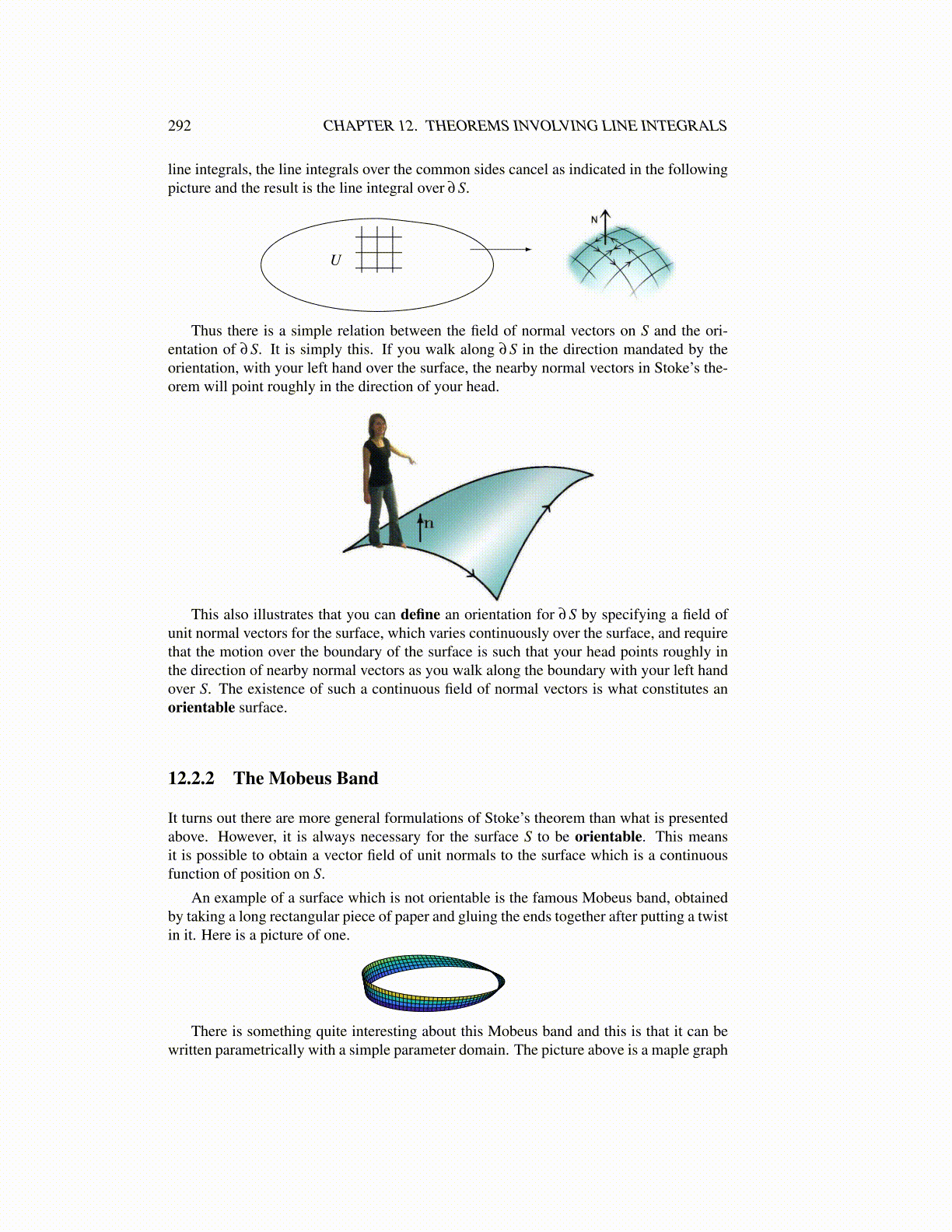
line integrals, the line integrals over the common sides cancel as indicated in the followingpicture and the result is the line integral over ∂S.
U
R
Thus there is a simple relation between the field of normal vectors on S and the ori-entation of ∂S. It is simply this. If you walk along ∂S in the direction mandated by theorientation, with your left hand over the surface, the nearby normal vectors in Stoke’s the-orem will point roughly in the direction of your head.
This also illustrates that you can define an orientation for ∂S by specifying a field ofunit normal vectors for the surface, which varies continuously over the surface, and requirethat the motion over the boundary of the surface is such that your head points roughly inthe direction of nearby normal vectors as you walk along the boundary with your left handover S. The existence of such a continuous field of normal vectors is what constitutes anorientable surface.
12.2.2 The Mobeus Band
It turns out there are more general formulations of Stoke’s theorem than what is presentedabove. However, it is always necessary for the surface S to be orientable. This meansit is possible to obtain a vector field of unit normals to the surface which is a continuousfunction of position on S.
An example of a surface which is not orientable is the famous Mobeus band, obtainedby taking a long rectangular piece of paper and gluing the ends together after putting a twistin it. Here is a picture of one.
There is something quite interesting about this Mobeus band and this is that it can bewritten parametrically with a simple parameter domain. The picture above is a maple graph