22 CHAPTER 1. REVIEW OF SOME LINEAR ALGEBRA
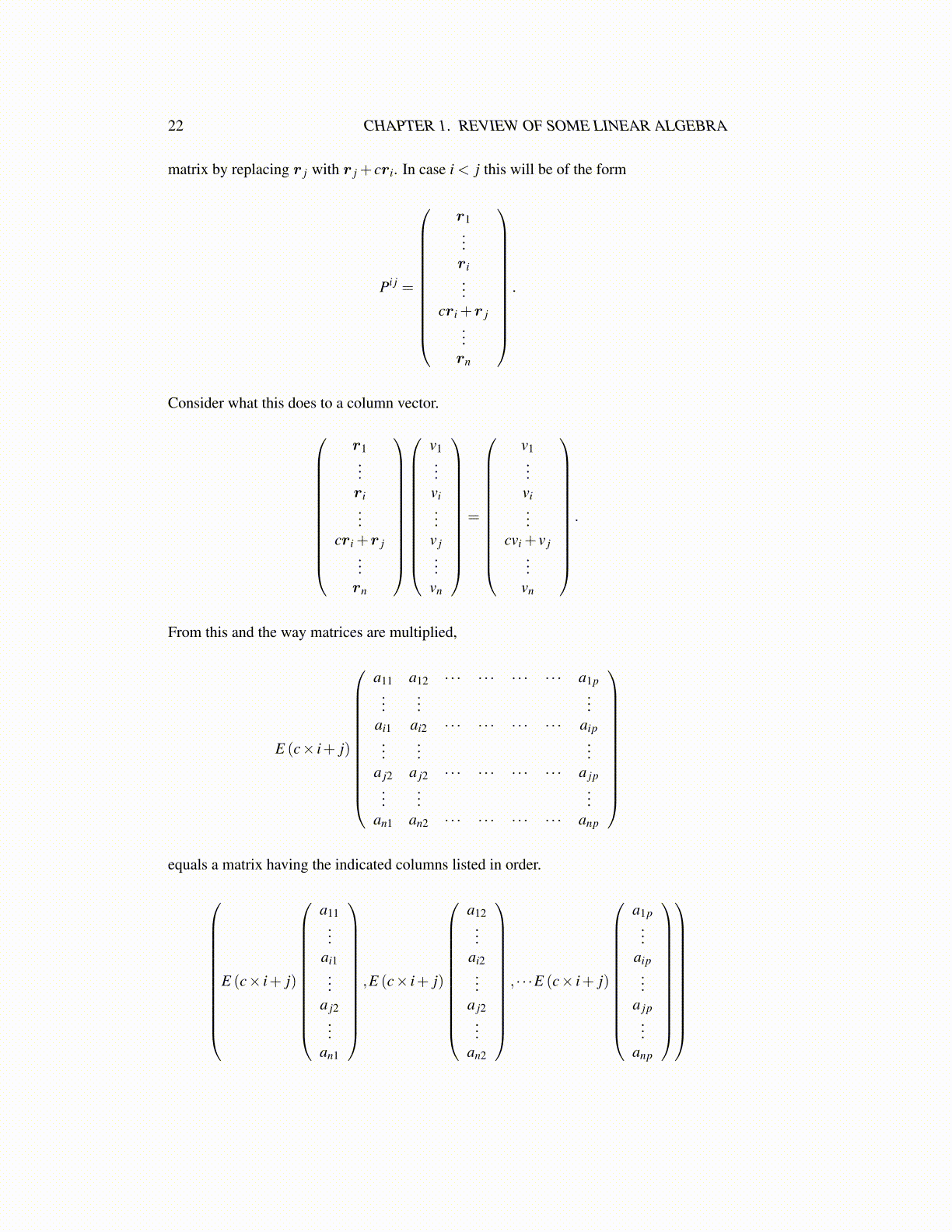
matrix by replacing r j with r j + cri. In case i < j this will be of the form
Pi j =
r1...ri...
cri +r j...rn
.
Consider what this does to a column vector.
r1...ri...
cri +r j...rn
v1...vi...
v j...
vn
=
v1...vi...
cvi + v j...
vn
.
From this and the way matrices are multiplied,
E (c× i+ j)
a11 a12 · · · · · · · · · · · · a1p...
......
ai1 ai2 · · · · · · · · · · · · aip...
......
a j2 a j2 · · · · · · · · · · · · a jp...
......
an1 an2 · · · · · · · · · · · · anp
equals a matrix having the indicated columns listed in order.
E (c× i+ j)
a11...
ai1...
a j2...
an1
,E (c× i+ j)
a12...
ai2...
a j2...
an2
, · · ·E (c× i+ j)
a1p...
aip...
a jp...
anp