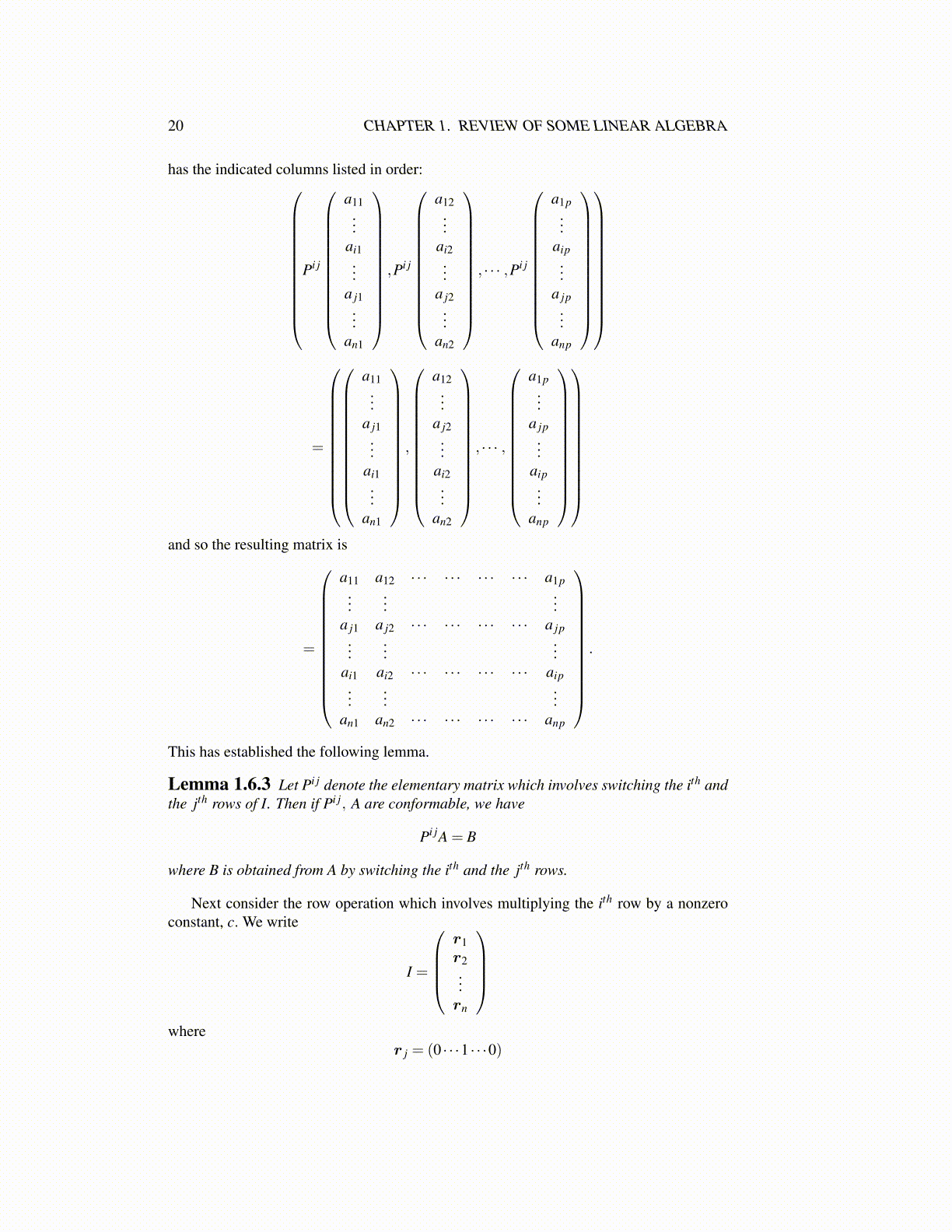
20 CHAPTER 1. REVIEW OF SOME LINEAR ALGEBRA

has the indicated columns listed in order:Pi j



a11...

ai1...

a j1...

an1

,Pi j



a12...

ai2...

a j2...

an2

, · · · ,Pi j



a1p...

aip...

a jp...

anp





=





a11...

a j1...

ai1...

an1

,



a12...

a j2...

ai2...

an2

, · · · ,



a1p...

a jp...

aip...

anp



and so the resulting matrix is

=



a11 a12 · · · · · · · · · · · · a1p...

......

a j1 a j2 · · · · · · · · · · · · a jp...

......

ai1 ai2 · · · · · · · · · · · · aip...

......

an1 an2 · · · · · · · · · · · · anp

.

This has established the following lemma.

Lemma 1.6.3 Let Pi j denote the elementary matrix which involves switching the ith andthe jth rows of I. Then if Pi j, A are conformable, we have

Pi jA = B

where B is obtained from A by switching the ith and the jth rows.

Next consider the row operation which involves multiplying the ith row by a nonzeroconstant, c. We write

I =

r1r2...rn

where

r j = (0 · · ·1 · · ·0)